Shear (1) - Transverse shear and composite action
- Si Shen

- May 19, 2019
- 3 min read
I have planned a series of blogs on the topic of shear. This is the first of the series, and it introduces the not-so-commonly known concept of ‘transverse shear’, and how it helps structures achieve composite action.
Transverse shear as a facilitator of composite action
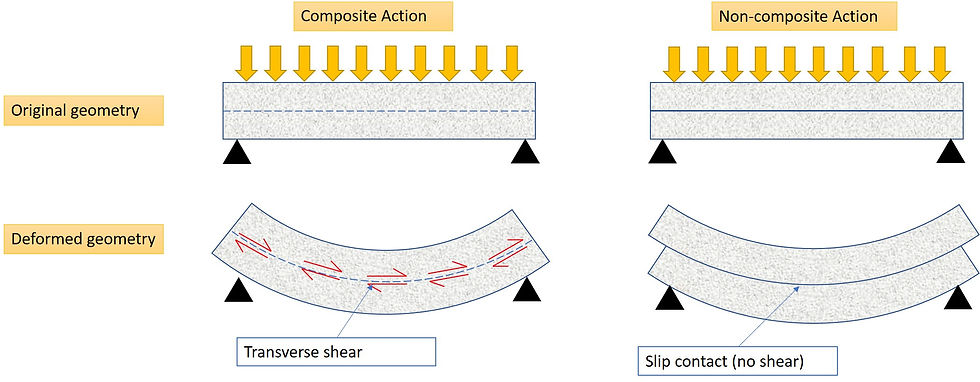
Composite action is an action where 1 + 1 is greater than 2. When two beams/slabs are simply stacked on top of each other, the structural capacity is simply the combination of the two; however, when the stacked beams are fastened at their interface, they work in composite, and achieve a structural capacity much greater than a simple adding of the two. A composite structure typically has less deflection and more bending capacity, or has less material/weight for the same given capacity to meet. The composite action relies on something called ‘transverse shear’ at the interface. Transverse shear is something that prevents slipping at the interface. More on transverse shear a bit later.
Composite action is commonly used in structural engineering – you will commonly notice the use of a concrete slab/deck on top of a series of steel I sections with shear studs. In a composite deck arrangement, each material does what it is best at: concrete takes compression, and steel takes tension.
Let me explain in a simple diagram below. Two stacked sections working in ‘combined’ action, rather than ‘composite’ action are shown in the diagram below. The deformed geometry of the ‘composite’ section is overlaid on top, as the red dash line. You can notice that to move from ‘combined’ action into ‘composite’ action, it is as if the top section is forced to shorten, whereas the bottom section is forced to lengthen. The shortening and elongating actions are both due to change in axial stress and strain. There is compressive stress in the top beam and tensile stress in the bottom beam. It is the transverse shear that transferred tensile stress from the top section into the bottom one.

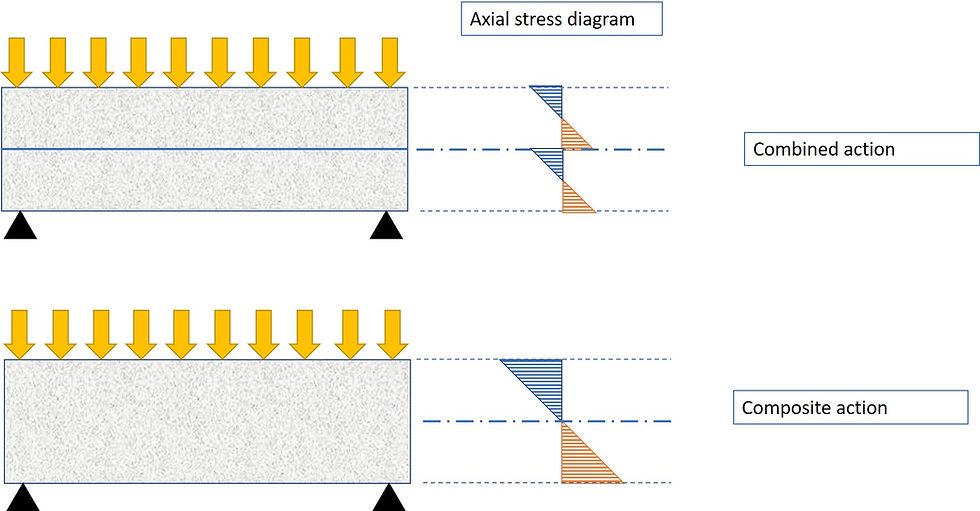
See the difference in axial stress between ‘combined action’ and ‘composite action’ below. You can notice that by moving into composite action, the top beam shifts towards higher and purer compression, whereas the bottom beam shifts towards higher and purer tension. This is what makes composite deck an attractive solution.
Transverse shear in concrete-to-concrete interface
Apart from composite deck, there is also use of transverse shear in pure concrete structures.
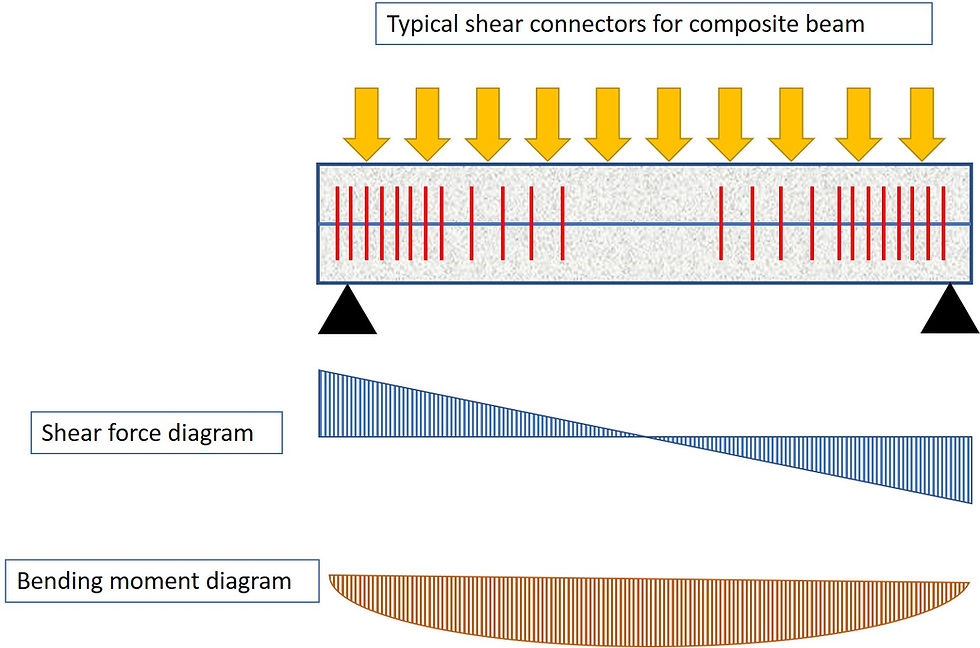
For deep beams, where it is not feasible to pour the entire section depth monolithically, shear connectors will need be designed to ensure composite action between the two sections cast at different times. If no shear connectors are used, each of the two sections will deform independently, slipping away from each other, and the top section which is typically unreinforced will start to crack. The intensity of the shear connectors is typically the highest at the ends and gradually reduces towards the centre. This is governed by the shear force diagram – note that analytical mechanics tells us that for any given element the vertical shear must be equal to its transverse shear in order for it to maintain equilibrium; in simpler terms transverse shear = vertical shear. See the diagram below. Note that the shear force diagram is the rate of change of the bending moment diagram - I want to discuss about this in more details in a future blog.
Building on the above, you would normally divide the pours evenly between two pours. But what if you don’t? or what if a cold joint is formed accidentally on site? Should the same amount of shear connectors be used regardless of where the joint between pours end up being?
The answer is NO.
The shear stress distribution is far from even across the entire depth. See the diagram below. As noted before, the change in axial stress is made possible and controlled by transverse shear. Axial stress builds up towards the axis of the beam and its transfer is facilitated by transverse shear. In other words, transverse shear makes changes in axial stress. The axial stress equates to the change in transverse shear stress. You can notice that at the extremities (top and bottom) the axial stress is the greatest and these are where the change rate in transverse shear being the greatest; around the axis, this is where the axial stress is smallest, and is also where the change rate in transverse shear being the smallest. The axial stress diagram represents the rate of change of the transverse shear diagram.
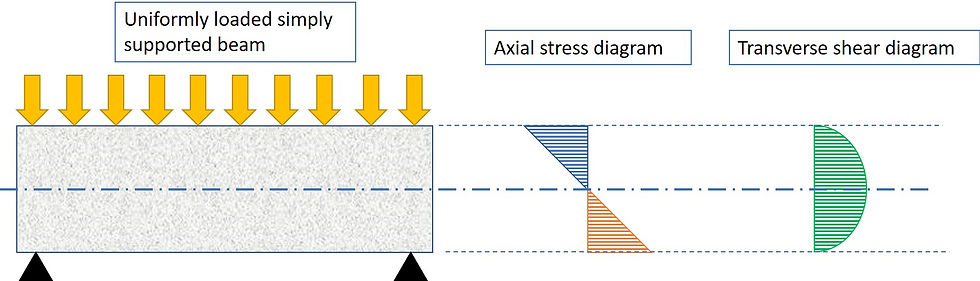
This diagram shows that the further away the joint is from the axis level, the less shear studs you will need to ensure composite action.
When designing the shear studs, the natural shear capacity of concrete-to-concrete interface should be taken into account in order to optimise the design. I will discuss the concrete-to-concrete interface shear in another blog in the near future.



Comments