Concrete behaviour in tension (1)
- Si Shen

- Mar 25, 2021
- 3 min read
Concrete is NOT linear-elastic
In finite element models, concrete is usually simplified down to a linear-elastic material. However, its real behaviour is far from the idealised linear-elastic one. Taking concrete as linear-elastic in both compression and tension is like treating it as metal and can lead to over-dosage of reinforcement.
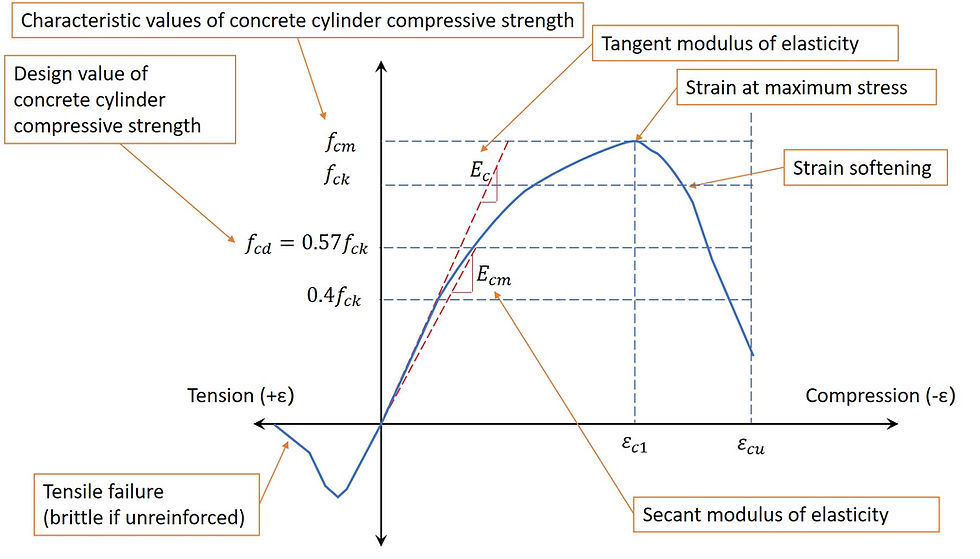
These two previous blogs discussed the full concrete stress-strain behaviour, with a main focus on the compression part.
However, the behaviour for concrete in tension is significantly different from that in compression – its effective stiffness depends on the level of cracking (strain). The higher strain, the lower the stiffness.
Concrete behaviour in tension
Concrete has the following properties in tension:
Concrete does not like tension. The compressive strength of concrete is much higher than its tensile strength (about 10 times). The stress-strain relationship for plain (unreinforced) concrete looks something like below:

Stiffness of concrete is different between tension and compression at high strain, with tensile stiffness being much lower due to cracking, explained below.
Cracks in concrete remain permanent and never heals even if the tension goes away.
From a design point of view, once cracked, concrete is no longer able to carry any tension (has zero tensile capacity and zero tensile stiffness) at the crack. The only material that remains to resist tension at the crack is the reinforcement.
Concrete wraps around and bonds to the reinforcement, and therefore reinforcement helps regulate cracking of concrete to a roughly equal spaced pattern, thus maintaining its partial stiffness even after cracking
Tension stiffening
Based on the above principles, in an analytical sense, the stiffness of a piece of reinforced concrete subject to tension could have 3 different status:
1. Until tension is high enough to lead to the development of cracks in concrete, the concrete and its reinforcing steel work together to resist tension, and therefore has high stiffness from steel and concrete combined.
2. At the location where concrete is cracked, only the reinforcing steel is left in place to resist the tension alone, and therefore the stiffness is much lower.
3. However, in real life, cracks in concrete do not take place everywhere, but progressively at certain spacings as tension increases. It is always the case that concrete remain attached to the reinforcing steel in between cracks due to bonding.
Therefore, when considered on a structural element scale, the effective stiffness of the cracked concrete almost always sits somewhere in between status (1) and status (2) as described above. This phenomenon is called ‘tension stiffening’.
Design stress-strain relationship of reinforced concrete in tension
Elastic stage – strictly speaking, the stress-strain curve at the elastic stage should be in the form of a minor softening curve (i.e. bending downwards slightly), but usually the softening is so small that it could be neglected. The end of the elastic stage is
Hardening stage – Concrete breaks its linear elastic behaviour upon the development of the first crack. As soon as the first crack appears, its effective stiffness starts to drop. The cracks start off being micro cracks, and with these progressively develop, concrete undergoes a phase of strain hardening behaviour. The hardening behaviour is a safety feature, demonstrated only in concrete that has at least code-minimum requirement (hence why design codes specify minimum reinforcement).
Softening stage – at the end of the hardening phase, a major crack will start to open up in concrete. As soon as this happens, concrete takes a major hit in its effective stiffness and enters its softening stage. The reinforcement helps distribute strain in concrete into a pattern of roughly evenly spaced cracks. These cracks will gradually open up one after another as strain increases. At the development of each crack, concrete takes a major hit on its effective stiffness and a step down is observed on the stress-strain diagram. The stress eventually reaches zero where concrete is so crumbled that it has virtually zero stiffness at all, even with tension stiffening. The full diagram is roughly a diving down parabolic curve – see below.

Some design codes (such as the Model Code 2010) simplifies this curve into a bi-linear behaviour – see below.

Bear in mind that the diagrams above are for concrete only. The reinforcing steel is still missing from the picture. Firstly, the design (simplified) stress-strain diagram of steel reinforcement looks like this:

Reinforced concrete is a composite material between concrete and steel. Therefore, for reinforced concrete in tension, the stiffness of the reinforcing bars needs to be added to the total effective stiffness, like below.

The composite stiffness is the stress-strain relationship can used in finite element analysis. Some software packages automate this dynamic stiffness calculation, whilst in other circumstances it is up to the engineer to work out the equivalent stiffness.


Comments